19世纪以前的课堂，大多是单调、重复、耗时的算术训练。德国布伦瑞克的一所小学里，一个普通的早晨，数学老师给全班同学出了个看似“磨时间”的题——把从1到100的所有整数加起来。

在老师的设想中，这是一道完美的拖堂题：100个数，乖乖从1加到100，别说是小学生，大人算起来也要好一阵。可事情没有按剧本发展——还没等粉笔在黑板上写完题意，一个瘦小的少年就把答案报了出来：“五千零五十。”

这个少年，就是后来被誉为“数学王子”的卡尔·弗里德里希·高斯（Carl Friedrich Gauss）。他没有像其他同学那样埋头逐个相加，而是抬起头，在脑海里“看见”了整个数列的规律。

他的思路是：把1和100配对，得到101；再把2和99配对，也是101；3和98，还是101。这样的配对一直持续下去——总共有50对，每对都是101。于是，总和就是50 × 101 = 5050。

不到一分钟，高斯就完成了老师原本要用半节课的“陷阱任务”。这一瞬间的灵光，直接孕育出一个通用公式：前n个整数的和 = n(n+1)/2。只要知道n，就能瞬间算出结果。

这个公式看似小巧，却藏着重要的启示：它不仅解决了有限数列的加法问题，还为后人打开了一扇通往“无穷”世界的大门——当n无限增大时，会发生什么？和会变成多大？那已经不是课堂小把戏，而是数学史上的深水区。

看似温柔的陷阱：调和级数的背叛

如果说高斯的故事告诉我们，“无穷”会让一个公式变得更加有趣，那么接下来的例子则证明，“无穷”也会让你的直觉彻底崩溃。

数学家们换了一个玩法：不再直接把 1、2、3、4……这些整数加起来，而是取它们的倒数——1，1/2，1/3，1/4，1/5……这就是著名的调和级数（Harmonic Series）。

乍一看，这个级数温柔得很：每一项都比前一项小，衰减速度肉眼可见。直觉告诉你，既然数字越来越小，累加的结果应该会逐渐趋向某个极限。

起初的确像是这样。第一项1，加上第二项1/2，总和是1.5；再加1/3，变成1.833…；加到第10项，也不过是2.928…——看起来快到“平稳区”了。更夸张的是，如果你想让这个和超过5，你得加上前83项；超过6，需要前227项；而要冲到10，你得耐心地把前1.2万项都加进去。增长得如此缓慢，很容易让人以为它最终会停下。

但14世纪的法国学者尼古拉·奥雷斯姆（Nicole Oresme）用一个精巧的分组方法，彻底粉碎了这个幻觉。

他把调和级数这样分组：

第1组：1

第2组：1/2

第3组：1/3 + 1/4

第4组：1/5 + 1/6 + 1/7 + 1/8

第5组：1/9 + … + 1/16

后面的组每次项数翻倍：16个、32个、64个……

看似随意的分组，却暗藏杀机：第三组中的每一项都 ≥ 1/4，所以这组的和 > 1/2；第四组每一项都 ≥ 1/8，这组的和又 > 1/2；第五组每一项 ≥ 1/16，这组的和依然 > 1/2……换句话说，除了开头的1，后面每一组都贡献了大于0.5的增量，而且这样的组是无限多的。

于是，调和级数的累加过程就像走楼梯——每走几步，就稳稳地上升半个台阶，永远不会停下。

结论无情而震撼：即使项越来越小，调和级数的总和依然会在无穷中失控地增长。数学家称它发散（Diverge）。

而这场“温柔陷阱”背后的逻辑，正为后来的一个问题埋下伏笔，能不能找到一个真正能收敛的无穷和？

第一道“驯服”的无穷和：三角数倒数

17世纪的欧洲，数学家们已经在无穷的海面上航行了一阵子。调和级数的背叛让他们警觉：不是所有看起来“越来越小”的数列都会乖乖收敛。但那也激发了一个新的好奇——有没有一种无穷加法，真的能“收口”到一个有限值？

荷兰科学家惠更斯（Christiaan Huygens）就抛出了这样一个挑战：把“三角数”的倒数加起来，会发生什么？

所谓“三角数”，是一种用圆点排成等边三角形的数字图案。

第一行1个点，是三角数1；

再加第二行2个点，总共3个点，是下一个三角数；

第三行3个点，总共6个点；

接着是10、15、21、28……

它们的数学公式很简单：第n个三角数 = n(n+1)/2。

惠更斯的问题是：把它们的倒数加起来——

1/1 + 1/3 + 1/6 + 1/10 + 1/15 + ……

这串无穷和，会不会收敛？如果收敛，又收敛到多少？

年轻的莱布尼茨（Gottfried Wilhelm Leibniz）接下了挑战，并很快发现了一个绝妙的拆分技巧。

他先写出这个和：

1/1 + 1/3 + 1/6 + 1/10 + ……

然后观察公式 n(n+1)/2，把分母里的n和n+1拆开，发现每一项都可以写成这样的差：

1/1 = 1 − 1/2

1/3 = 1/2 − 1/3

1/6 = 1/3 − 1/4

1/10 = 1/4 − 1/5

……

神奇的事情发生了：当你把这些项一项一项加起来，所有“中间项”都会前后抵消——1/2被减掉又加回来，1/3也是如此，1/4也是……唯一幸存的，是开头的那个“1”。

结果，整个无穷和在抵消之后，只剩下：

S/2 = 1

于是，S = 2。

这是一个重要的分水岭。它告诉数学家们：无穷相加并非注定失控，只要衰减得够快、结构足够巧妙，就能收敛到一个确定的值。

而且，莱布尼茨的方法给了他们一件新武器——通过结构拆分和连锁抵消，驯服原本看似不可控的无穷级数。

接下来，这件武器很快就被用在了一个更大、更棘手、也更传奇的问题上——巴塞尔问题。那是一头沉睡百年的“数学怪兽”，直到遇见一位史上最强的大杀器：欧拉。

巴塞尔问题的百年之谜

如果说三角数倒数的收敛给了数学家信心，那么下一个挑战，则让他们一次次撞在了无形的天花板上。

这一次，分母不再是三角数，而是平方数：

1/1² + 1/2² + 1/3² + 1/4² + 1/5² + ……

这些数字看上去比调和级数要“温顺”得多——衰减得快得多，而且和三角数倒数一样，项与项之间的差距迅速拉大。于是大家猜测，这个和肯定是有限的。

证明它收敛并不难。17世纪末，瑞士数学家雅各布·伯努利（Jacob Bernoulli）就用“比较法”做到了：

既然三角数倒数的无穷和是 2，而平方数倒数的每一项都比三角数倒数对应项更小，那它的总和一定小于 2。

问题在于——它究竟等于多少？

雅各布没能找到答案。他甚至在论文末尾写下了公开求助：“如果有人能找到这个值，并告知我们，我们将不胜感激。”

从那一刻起，这个看似无害的问题，就像一枚火种，在欧洲数学界悄然发酵。由于雅各布来自巴塞尔，这个谜题被称作“巴塞尔问题”。

它的表面很简单：

但简单的外衣下，藏着的是数学的硬骨头。你可以算前10项、前100项，得到一个越来越接近的数字——1.549… 1.634… 1.643…——它似乎在逼近某个神秘常数，可它就是不肯“自报家门”。

伯努利家族的另一位天才——约翰·伯努利（Johann Bernoulli）——也没能破解。更让人绝望的是，莱布尼茨、惠更斯等一线高手也束手无策。一百多年间，没人能找出确切的闭合公式。

巴塞尔问题成了数学家的集体执念：它没有奇怪的定义，没有复杂的背景，只是赤裸裸的“加一串分数”——可这串分数，就像有魔咒一般，把所有聪明人挡在了门外。

直到18世纪30年代，一个年轻人拿起了它。

他出身巴塞尔，数学启蒙老师正是约翰·伯努利本人；他才二十出头，就已经在数学前沿发光发热；他的思维天马行空，不受旧方法的束缚——他叫莱昂哈德·欧拉（Leonhard Euler）。

而他，正要用一次惊天的跨界联想，让巴塞尔问题的百年迷雾，在一瞬间化为清晰的阳光。

欧拉的惊世一跃

1730年代的巴塞尔，莱昂哈德·欧拉年仅二十出头，刚从伯努利兄弟的课堂毕业，便带着一股不服输的锐气闯进了数学的核心战场。巴塞尔问题，这个困扰欧洲数学界百年的死结，在他眼中不是绝壁，而是通往高峰的阶梯。

欧拉没有沿用前人那套“对比、夹逼、近似”的老路，而是转了一个极为大胆的念头——把这个加分数的问题，和一个三角函数扯上关系。

他从正弦函数 sin⁡x 出发。学生时代的他早已熟练掌握泰勒展开：

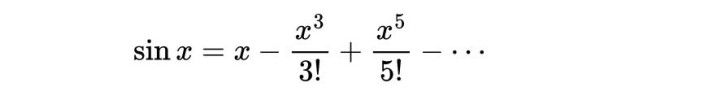
于是，(sin⁡x)/x 就是一个关于 x^2 的无限多项式。

另一方面，他又想起了代数中一个简单但威力巨大的事实：一个多项式可以分解为与它的“根”相关的乘积。比如，一个二次多项式 P(x)有两个根 a 和 b，它就可以写成 (1−x/a)(1−x/b)的形式。

如果多项式可以这样分解，那无限多项式呢？欧拉凭着惊人的直觉，认为这同样适用于(sin⁡x)/x这样的“无限多项式”。

正弦函数的零点大家都知道：除了 x=0，其余都是 ±π，±2π，±3π，…。于是欧拉将 (sin⁡x)/x 写成了一个惊人的无限乘积：

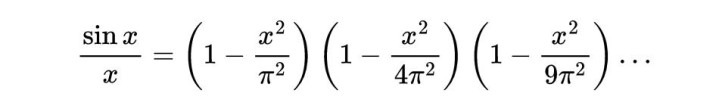
接下来是魔术时刻——他把这个乘积“假装”像普通多项式一样展开，比较两边的 x^2 项系数。

一边是泰勒展开的 x^2 项系数：

另一边是无限乘积的 x^2 项系数：它来自于

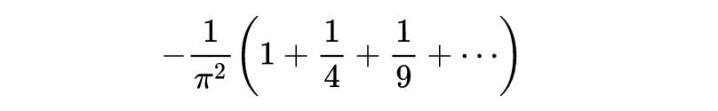
让这两个系数相等，负号对消，结果震撼人心：

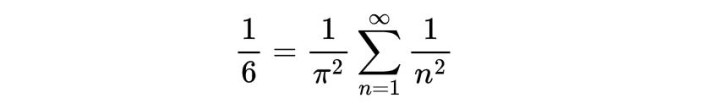
于是——

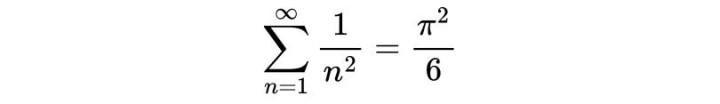
巴塞尔问题的百年迷雾，在一瞬间被刺破。一个看似毫不相关的圆周率 π，竟然深藏在整数平方倒数的和里。

1735年，欧拉公布了这个结果，数学界轰动不已。雅各布·伯努利早在几十年前的感慨“若有人找到答案，我们将不胜感激”，终于等来了回音，而且答案的美，超乎任何人的想象。

更令人惊叹的是，欧拉并未止步于此。他用同样的方法，找到了所有偶数次幂的倒数和公式：

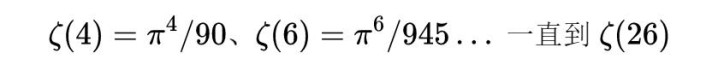
而奇数次幂的倒数和，却像一道新的铁门，至今没人找到它的钥匙。

未解的另一半与黎曼的远方

欧拉的胜利，不只是解开了巴塞尔问题，它更像是在数学世界里炸开了一枚信号弹——无穷级数的背后，潜藏着比想象中更宏大的结构。

用他的手法，所有偶数次幂的倒数和都被一网打尽，每一个偶数次的公式，都是干净到近乎诗意的分数，分子里安然坐着一个偶数次的 π，分母则是一连串整齐的常数。

可一旦幂次变成奇数，画面就变了味。

这就是著名的阿佩里常数（Apéry’s constant）。欧拉同样写得出它的数值近似，可等式右边却没有出现任何像 π^2/6 那样的简洁表达。几个世纪过去，它依然没有优雅的闭合公式——不仅 ζ(3)如此，ζ(5)，ζ(7)等等全都顽固地沉默着。

数学家逐渐意识到，这些和式并非一盘散沙，而是属于一个更庞大的家族：黎曼 ζ 函数

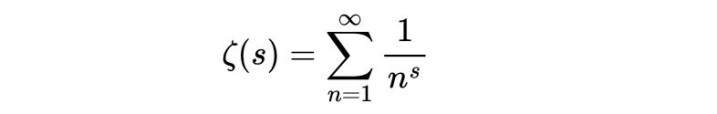
这里的 s，可以是任何复数。当 s 是偶数正整数时，欧拉的成果闪闪发光；当 s 是奇数正整数时，它们则像深海里的暗流，不肯向人类吐露全部秘密。

1859年，德国数学家伯恩哈德·黎曼（Bernhard Riemann）在一篇不到十页的论文中，将 ζ 函数推进到了一个更惊心动魄的维度——他把它延拓到了整个复平面，并在分析它的零点分布时，提出了一个至今无人攻破的猜想：黎曼假设。

黎曼假设看似离巴塞尔问题很远，但它触及的却是同一根神经：素数的分布。ζ 函数的性质，与素数的规律紧密交织在一起。若黎曼假设成立，我们将能以近乎外科手术的精确度刻画素数的出现节奏。这不仅是数论的皇冠，更被誉为数学界的珠穆朗玛峰——美国克雷数学研究所为它悬下了一百万美元的悬赏。

从高斯课堂里的 1+2+…+100，到欧拉手中的 π^2/6，再到黎曼 ζ 函数延伸出的世纪难题，这条路横跨了两百多年，串联起无数数学家的心血与执念。

偶数幂的答案，像白天的星星，已被看得清清楚楚；奇数幂的谜团，依旧在夜色里沉睡。而那片夜色深处，也许正藏着数学未来最炽热的光。